Stepping down into the Ocaml Mines - UIUCTF 2025 Writeup

3rd August, 2025

This writeup and solution is a combined effort from me and my teammate “e-” (Elemental) as part of CTF Academy. I decided to keep this writeup a bit comprehensive because it took us embarrassingly long to solve this challenge, but it allowed me to learn a lot about how Ocaml works.

This rev challenge is based around a pretty old functional programming language known as “Ocaml” which I was completely unaware of before this CTF. Personally I found this challenge pretty interesting which helped me discover a niche language, understand it and then reverse the logic to get the flag!

Challenge #1: WeirdCaml

Category: rev
Author: n8

Brief info about the challenge and Ocaml

The challenge gives us a file with a long list of type definitions, which to be honest were a bit hard to understand for me.

type b_true
type b_false
type 'a val_t =
 | T : b_true val_t
 | F : b_false val_t

This snippet represents the first part of the problem, let’s break it down to understand what’s going on. The challenge file declares two empty types called b_true and b_false, at no point in the file are these types used for any variables, these are purely used as empty type markers or boolean flags. You can think of them as undefined macros in C:

#DEFINE b_true
#DEFINE b_false

Then there’s another type definition, ’a val_t. This is interesting because the type definition here is ambiguous and is dependent on type of a hence the apostrophe before it: ’a. This is known as a GADT (Generalized algebraic datatypes) in Ocaml. This pattern allows us to create polymorphic types by passing a ambiguous type parameter.

type 'a val_t =
 | T : b_true val_t
 | F : b_false val_t

T and F are called constructors for this GADT, this means that we can only invoke constructor T when ’a is set to b_true and constructor F only when ’a is set to b_false.

Now let’s look at the next part of the challenge:

type ('a, 'b, 'c, 'd) p1_t =
 | P1_1 : b_true val_t -> ('a, b_true, 'c, 'd) p1_t
 | P1_2 : b_true val_t -> ('a, 'b, b_true, 'd) p1_t
 | P1_3 : b_true val_t -> ('a, 'b, 'c, b_true) p1_t
 | P1_4 : b_true val_t -> (b_false, 'b, 'c, 'd) p1_t

now that we understand how GADT’s work, the challenge defines a ton of GADT’s in the form of px_t where x ranges from 1 to 1435 to be precise, but this time these GADT’s define 4 type parameters, and 4 constructors which determines different constraints on these type parameters.

For example: calling p1_t with constructor P1_1 with value T (b_true val_t) means that among the returned type parameters ’b has to be of the type b_true while ’a, ’c, ’d can be ambiguous types. In the given problem every constructor restricts one output type while the other 3 type parameters can be ambiguous types.

Taking a look at type puzzle

Finally we have one last type definition called puzzle, this defines the core problem in our CTF so let’s have a look at first part of puzzle:

type puzzle =
 Puzzle :
 'flag_000 val_t * 
 'flag_001 val_t * 
 'flag_002 val_t *
 …
 'flag_103 val_t *
 'a val_t * 
 'b val_t * 
 'c val_t *
 …
 'z val_t *
 'a1 val_t * 
 'a2 val_t * 
 'a3 val_t *
 …
 'a147 val_t *

type puzzle is another GADT, and a massive one which starts by defining a single constructor called Puzzle which binds a bunch of type variables divided in 3 parts:

'flag_000 to ‘flag_103 (flag bits encoded in the form of T/F)
‘a to ‘z (idk why there are types from a to z)
‘a1 to ‘a147 (more supporting variable types)

Since there are 104 type variables of the format flag_XXX, we can assume that these constitute individual flag bits, so 104/8 = 13 flag bytes. The other type variables are just supporting variables which help us set constraints for the flag type variables.
PS: Something which bugged me for a long time in this problem was why are there type variables ranging from ’a to ’z when they have nothing to do with the flag directly, before solving the problem I kept thinking they have some connection to the flag which kept putting me off-track.

Now let’s look at next part of type puzzle:

('a, 'flag_016, 'flag_038, 'flag_040) p1_t *
('a, 'flag_016, 'flag_038, 'flag_040) p2_t *
('a, 'flag_016, 'flag_038, 'flag_040) p3_t *

We find a bunch of type annotations, which take some type parameters and match it against the allowed type definitions for that type. For example: if we look at the passed type parameters for this annotation: (‘a, ‘flag_016, ‘flag_038, ‘flag_040) p1_t * this means that for this expression to be valid it has to returned by invoking of the constructors from p1_t’s GADT.

That means this condition has to match against one of these 4 constraints for it to be a valid type:

type ('a, 'b, 'c, 'd) p1_t =
 | P1_1 : b_true val_t -> ('a, b_true, 'c, 'd) p1_t
 | P1_2 : b_true val_t -> ('a, 'b, b_true, 'd) p1_t
 | P1_3 : b_true val_t -> ('a, 'b, 'c, b_true) p1_t
 | P1_4 : b_true val_t -> (b_false, 'b, 'c, 'd) p1_t

Now we have a whole overview of what constructor Puzzle in type puzzle is, by definition it defines a humungous tuple where each type is concatenated by an asterisk * which is like an AND condition.

So for the whole type puzzle to be valid, every single type inside the tuple should be a valid type.

Now this statement has some interesting implications, since all the type variables are defined with val_t they can only be of constructor type T or type F from val_t’s GADT. Now we can resolve this problem by using a constraint solver and putting in all our constraints and try to find a solution which satisfies them.

Solution

For our solve script we’ll use Z3 as our constraint solver, but first we need to set variables and build constraints for Z3 to work.

Making variables

As we saw earlier we have 3 types of type variables, even though we only care about the flag_XXX variables we need to give Z3 all of them as the flag types depend on the other supporting type variables. Since all these types are of type val_t which can only be defined with type T or type F, we can treat them as booleans or more conveniently in Z3 as BitVectors of size 1.

def make_vars():
    flag = {}

    for i in range(104):
    var_name = 'flag_' + str(i).rjust(3, '0')
    flag[var_name] = BitVec(var_name, 1)

    for i in range(1, 148):
    var_name = 'a' + str(i)
    flag[var_name] = BitVec(var_name, 1)

    for i in range(97, 123):
    var_name = chr(i)
    flag[var_name] = BitVec(var_name, 1)

    return flag

flag = make_vars()

For convenience we just bundled them up and put them in a dictionary.

Parsing conditions from constructors

Let’s look at a sample constraint for this type definition: (‘a, ‘flag_016, ‘flag_038, ‘flag_040) p1_t *

Looking at this above constraint for type p1_t we can’t really say much because we don’t know which constructor resulted in this type declaration. But what we do know that for it to be a valid type declaration it has to come from one of the 4 constructors of p1_t i.e. P1_1 to P1_4. Which means we can combine these 4 conditions with a single OR operation.

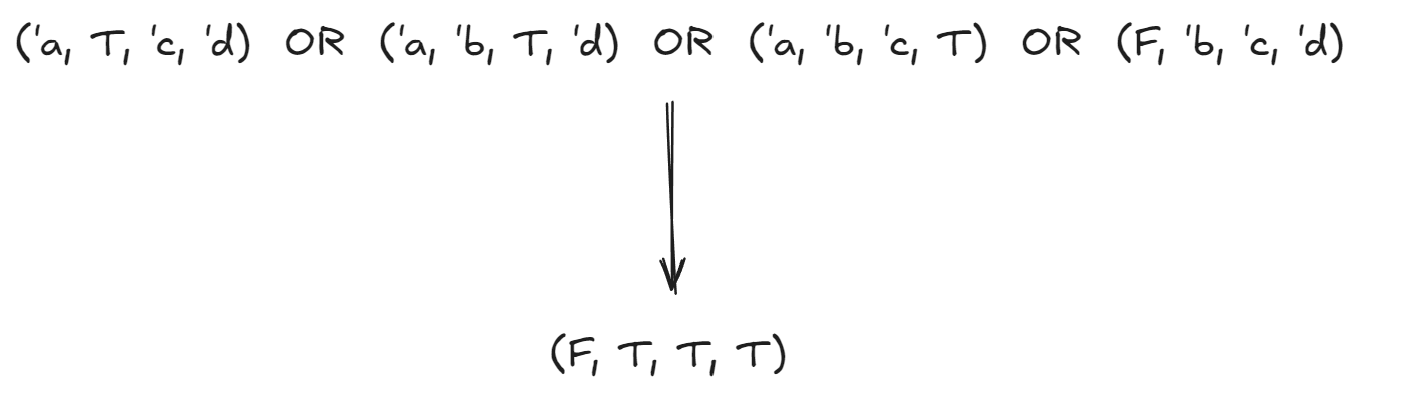
Since all other type variables are ambiguous we can condense all 4 possible constructors into a single condition by just OR-ing them. Similarly we can do the same for all of the type variables of the form px_t and store them in a dictionary.

def make_constraints(raw_string):
    chunks = raw_string.split("type ")
    chunks = chunks[1:]
    filtered = []
    p_dict = {}
    for i in range(len(chunks)):
        data = chunks[i].lstrip().rstrip().split('\n')
        data[0] = data[0].replace('=', "").lstrip().rstrip()
        temp = data[0].split(" ")
        data[0] = temp[-1]
        key = data[0]
        value = [0] * (len(data)-1)
        for j in range(1, len(data)):
            rules = data[j].split(" ")
            rules = rules[8:12]
 
        for k in range(len(rules)):
            if 'b_true' in rules[k]:
              value[k] = 1
            if 'b_false' in rules[k]:
              value[k] = 0
        
        p_dict[key] = value

    return p_dict

p_dict = make_constraints(raw_px_t)

Building constraints for Z3

After we are done dealing with our polymorphic constructors we can now move on to looking at constraints for our type variables. This part was mostly done by my teammate “e-” so I’ll just try to summarize his approach. Before building the constraints I want to point out something very important he mentioned which will help us later on.

('a, 'flag_016, 'flag_038, 'flag_040) p1_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p2_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p3_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p4_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p5_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p6_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p7_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p8_t *
 ('a, 'b, 'flag_068, 'flag_071) p9_t *
 ('a, 'b, 'flag_068, 'flag_071) p10_t *
 ('a, 'b, 'flag_068, 'flag_071) p11_t *
 ('a, 'b, 'flag_068, 'flag_071) p12_t *
 ('a, 'b, 'flag_068, 'flag_071) p13_t *
 ('a, 'b, 'flag_068, 'flag_071) p14_t *
 ('a, 'b, 'flag_068, 'flag_071) p15_t *
 ('a, 'b, 'flag_068, 'flag_071) p16_t *
 ('b, 'a60, 'flag_101, 'flag_091) p17_t *
 ('b, 'a60, 'flag_101, 'flag_091) p18_t *
 ('b, 'a60, 'flag_101, 'flag_091) p19_t *
 ('b, 'a60, 'flag_101, 'flag_091) p20_t *
 ('b, 'a60, 'flag_101, 'flag_091) p21_t *
 ('b, 'a60, 'flag_101, 'flag_091) p22_t *
 ('b, 'a60, 'flag_101, 'flag_091) p23_t *
 ('b, 'a60, 'flag_101, 'flag_091) p24_t *
 ('a60) p25_t *

Look at this small snippet which defines constraints on types from p1_t to p25_t, we can definitely see a pattern here where every 8 consecutive types use the same variable but all of them have a type parameter in common, but after this these variables don’t appear. My teammate’s idea was to classify this as a single group since all these type variables are dependent on each other and are bound by a single type variable which we know for sure is T or F i.e. a60 in this case.

PS: I think it’s not necessary to make groups for this challenge, it’s just easier to feed it to Z3 if we do it this way.

Feeding constraints to Z3

Now that we know how to segregate our constraints into groups, we need to parse it and let Z3 know about the constraints. As discussed earlier every line of constraint can be resolved with an Or operator in Z3 since any one constructor needs to be valid. Now we need to chain all these constraints together with an And operator in Z3, since all these type variables need to be valid at the same time. To better visualize it this is how the first 4 constraints would look like without grouping:

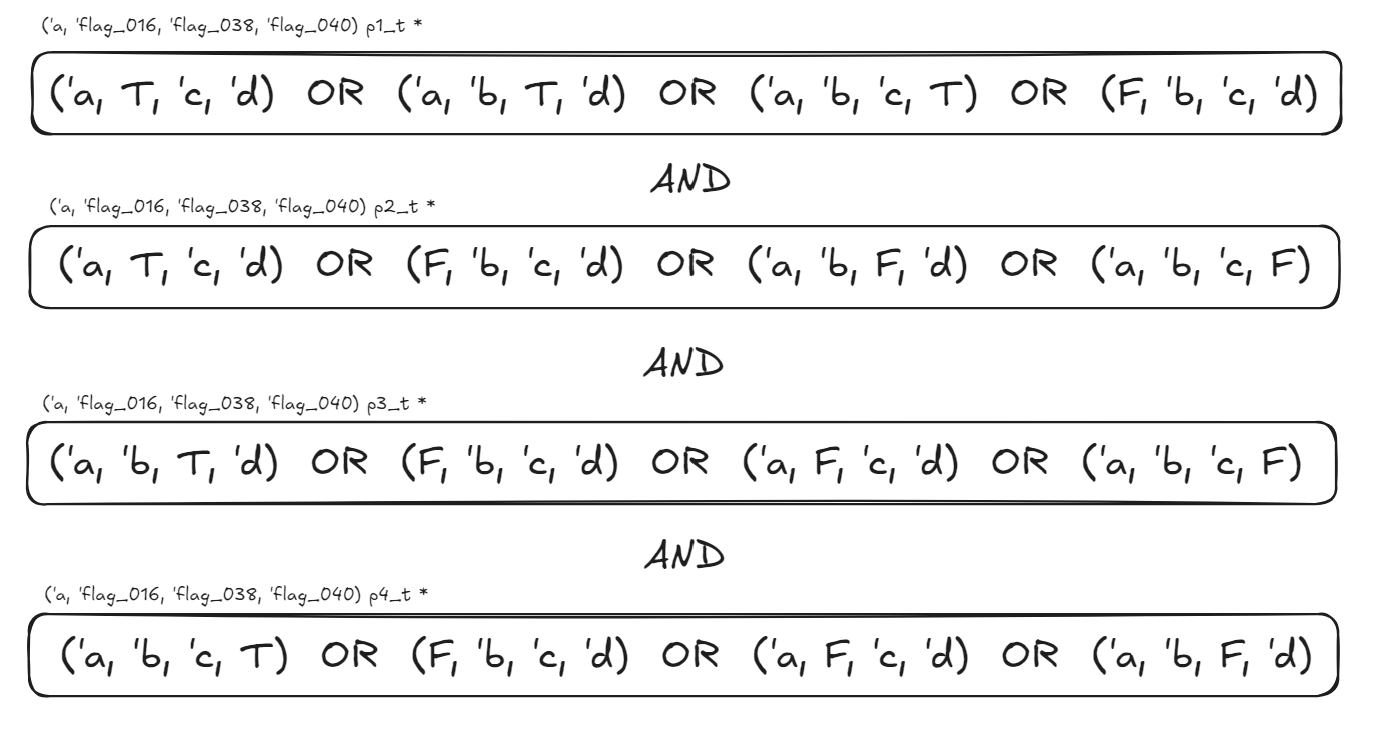
Code for parsing groups and feeding constraints to Z3:

def parse_group(input):
    group = []
    
    lines = input.split('*')
    for i in range(len(lines)):
        lines[i] = lines[i].lstrip()
        lines[i] = lines[i].rstrip()
    
    if lines[-1] == "":
        lines = lines[:-1]
 
    for i in range(len(lines)):
        data = lines[i].split(" ")
        for j in range(len(data)):
            data[j] = data[j].replace("(", "").replace(")", "").replace(",", "").replace("'", "")
 
        # px_t member
        px_t = data[-1]
        px_t = p_dict[px_t]
        members = data[:-1]
        for j in range(len(members)):
            members[j] = flag[members[j]]
        group.append(check_px_t(px_t, members))
  
    #print(And(*group))
    return And(*group)

def check_px_t(px_t, nominee): # p1_t = F T T T
    equality = [px_t[i] == nominee[i] for i in range(len(px_t))]
 
    res = Or(*equality)
 
    return res

s = Solver()
s.add(parse_group(raw_input) == True)

Now that we’re done adding our constraints time to let it rip and see if it is even satisfiable!

Final solution:

raw_input = """
 ('a, 'flag_016, 'flag_038, 'flag_040) p1_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p2_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p3_t *
 ('a, 'flag_016, 'flag_038, 'flag_040) p4_t *
…
 ('a57) p1435_t
"""
raw_px_t = """
type ('a, 'b, 'c, 'd) p1_t =
 | P1_1 : b_true val_t -> ('a, b_true, 'c, 'd) p1_t
 | P1_2 : b_true val_t -> ('a, 'b, b_true, 'd) p1_t
 | P1_3 : b_true val_t -> ('a, 'b, 'c, b_true) p1_t
 | P1_4 : b_true val_t -> (b_false, 'b, 'c, 'd) p1_t
…
type ('a) p1435_t =
 | P1435_1 : b_true val_t -> (b_false) p1435_t
"""

def make_vars():
    flag = {}

    for i in range(104):
    var_name = 'flag_' + str(i).rjust(3, '0')
    flag[var_name] = BitVec(var_name, 1)

    for i in range(1, 148):
    var_name = 'a' + str(i)
    flag[var_name] = BitVec(var_name, 1)

    for i in range(97, 123):
    var_name = chr(i)
    flag[var_name] = BitVec(var_name, 1)

    return flag

flag = make_vars()

def make_constraints(raw_string):
    chunks = raw_string.split("type ")
    chunks = chunks[1:]
    filtered = []
    p_dict = {}
    for i in range(len(chunks)):
        data = chunks[i].lstrip().rstrip().split('\n')
        data[0] = data[0].replace('=', "").lstrip().rstrip()
        temp = data[0].split(" ")
        data[0] = temp[-1]
        key = data[0]
        value = [0] * (len(data)-1)
        for j in range(1, len(data)):
            rules = data[j].split(" ")
            rules = rules[8:12]
 
        for k in range(len(rules)):
            if 'b_true' in rules[k]:
              value[k] = 1
            if 'b_false' in rules[k]:
              value[k] = 0
        
        p_dict[key] = value

    return p_dict

p_dict = make_constraints(raw_px_t)
# pprint(p_dict)

def parse_group(input):
    group = []
    
    lines = input.split('*')
    for i in range(len(lines)):
        lines[i] = lines[i].lstrip()
        lines[i] = lines[i].rstrip()
    
    if lines[-1] == "":
        lines = lines[:-1]
 
    for i in range(len(lines)):
        data = lines[i].split(" ")
        for j in range(len(data)):
            data[j] = data[j].replace("(", "").replace(")", "").replace(",", "").replace("'", "")
 
        # px_t member
        px_t = data[-1]
        px_t = p_dict[px_t]
        members = data[:-1]
        for j in range(len(members)):
            members[j] = flag[members[j]]
        group.append(check_px_t(px_t, members))
  
    #print(And(*group))
    return And(*group)

def check_px_t(px_t, nominee): # p1_t = F T T T
    equality = [px_t[i] == nominee[i] for i in range(len(px_t))]
 
    res = Or(*equality)
 
    return res

s = Solver()
s.add(parse_group(raw_input) == True)

def bits_to_ascii(bit_string):
    flag = ""
    for i in range(0, 104, 8):
        val = int(bit_string[i:i+8], 2)
        flag+=chr(val)
    return flag
  
bit_string = ""
if s.check() == sat:
    m = s.model()
    for i in range(104):
        bit = m[flag['flag_%.3d' % i]].as_long()
        print(bit, end="")
        bit_string+=str(bit)
    print()
    print(f"Decoded bit string: {bits_to_ascii(bit_string)}")
else:
  print("unsat")

Final flag: uiuctf{sat_on_a_caml}

Something to think about: Why does challenge say flag will be printed to stderr?

This is like a bonus section, but very important to understand how this challenge works under the hood and more importantly why it takes so long to compile.

After our first failed attempt to get the flag, I started wandering in different rabbit holes and one question that prompted in my head was
“Why does the challenge say that the flag will be printed out in stderr?”

Even if the script takes too long why stderr and not stdout. So I decided to explore a bit and using some of the conditions from the original ocaml file I decided to build another toy ocaml file to play around the code a little bit.

Since there were a lot of type definitions and constraints in the original file, I decided to put only a handful to test out how things play out, here’s the toy file:

type b_true
type b_false
type _ val_t =
 | T : b_true val_t
 | F : b_false val_t

type ('a, 'b, 'c, 'd) p1_t =
 | P1_1 : b_true val_t -> ('a, b_true, 'c, 'd) p1_t
 | P1_2 : b_true val_t -> ('a, 'b, b_true, 'd) p1_t
 | P1_3 : b_true val_t -> ('a, 'b, 'c, b_true) p1_t
 | P1_4 : b_true val_t -> (b_false, 'b, 'c, 'd) p1_t
type ('a, 'b, 'c, 'd) p2_t =
 | P2_1 : b_true val_t -> ('a, b_true, 'c, 'd) p2_t
 | P2_2 : b_true val_t -> (b_false, 'b, 'c, 'd) p2_t
 | P2_3 : b_true val_t -> ('a, 'b, b_false, 'd) p2_t
 | P2_4 : b_false val_t -> ('a, 'b, 'c, b_false) p2_t
type ('a, 'b, 'c, 'd) p3_t =
 | P3_1 : b_true val_t -> ('a, 'b, b_true, 'd) p3_t
 | P3_2 : b_false val_t -> (b_false, 'b, 'c, 'd) p3_t
 | P3_3 : b_true val_t -> ('a, b_false, 'c, 'd) p3_t
 | P3_4 : b_true val_t -> ('a, 'b, 'c, b_false) p3_t

type puzzle =
 Puzzle :
 'flag_000 val_t *
 'flag_001 val_t *
 ('a, 'flag_000, 'flag_001, 'flag_002) p1_t *
 ('a, 'flag_000, 'flag_001, 'flag_002) p2_t *
 ('a, 'flag_000, 'flag_001, 'flag_002) p3_t
 -> puzzle

let check1 (f: puzzle) = function
 | Puzzle _ -> .
 | _ -> ()

If we focus on the last 3 lines where we define a function check which takes an argument f of type puzzle, and it returns a function which tries to pattern match constructor Puzzle with _. The . in Ocaml is very interesting because it represents a refutation case in Ocaml, it’s a way of telling the Ocaml compiler that “Prove that this branch is impossible to reach if a type puzzle is passed as an argument”.

Since the value we passed is indeed of type puzzle, the only way to prove it is impossible to reach is to prove that the constructor Puzzle is invalid or that there is no combination of type variables which satisfy this type. The way the Ocaml compiler deals with this is by trying to find a solution to determine if it is actually unreachable and if there is a solution it prints out the combination in stderr.

And since the challenge is designed in a way that it has a solution, this is what we get when we try to compile our toy ocaml file:

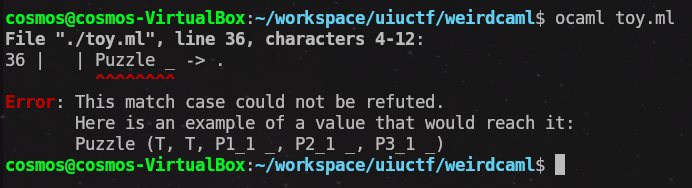
This represents a valid combination of types, which in our case would be the bit representation of all the flag type variables. But since, in our original problem we have a massive tuple with a ton of conditions, the Ocaml compiler tries every possible combination to refute that this branch is impossible which takes forever, therefore the goal is to optimize this using Z3 and get the flag!

Challenge #2: Nocaml

Category: misc
Author: n8

This was another Ocaml challenge in the miscellanous category in the CTF, but sadly I could only solve this after the CTF ended. Nevertheless this was another cool challenge which made me dig around Ocaml a bit more to finally get the flag.

The challenge prompt is simple “just cat the flag” using your Ocaml script but there’s a small problem in doing that since the given challenge file starts by setting everything to null, making all the standard library functions impossible to use. Functions such as open_in (Open file), print_endline (write) are basically useless now. The challenge script also sets a lot of core modules like Stdlib, Printf to empty structs which makes them unusable and since most of the I/O functions are defined in Stdlib we’re pretty much cooked without it.

let stdin = ()
let stdout = ()
let stderr = ()
let print_char = ()
let print_string = ()
let print_bytes = ()
let print_int = ()
let print_float = ()
let print_endline = ()
let print_newline = ()

module Stack = struct end
module StdLabels = struct end
module Stdlib = struct end
module String = struct end
module StringLabels = struct end
module Sys = struct e

But since most of these library functions rely on some sort of lower-level C functions to execute, we can still craft our exploit by directly calling into those lower-level functions. During the CTF I had a hard time finding documentation for these functions and gave up on this challenge, but after peeking at the source code I realized this challenge is not that hard.

Solution

As I said earlier, instead of relying on the library functions we need to make our own custom functions which mimic their functionality and call into the lower-level C functions. Let’s look at how the library functions are defined in the first place in Ocaml source code: https://github.com/ocaml/ocaml/blob/trunk/stdlib/stdlib.ml

Let’s dissect how a stdlib function is defined:

external output_char : out_channel -> char -> unit = "caml_ml_output_char"

If you’re unfamiliar with the Ocaml syntax, let me break it down for you. In Ocaml the function definition starts with the function_name and then the type of the parameters it takes separated by a colon and ->, and the last type parameter is for the function output. So this essentially defines a function called output_char which takes 2 args.: first one of type out_channel (similar to a file_descriptor) and second one a character (char to print) and it returns a value of type unit which similar to return void in C.

The external keyword helps Ocaml interface with C functions and I think in this case it uses a lower-level C function called caml_ml_output_char.

Now that we know how it works let’s try to replicate the same logic using our custom functions. Before making our custom functions let’s see how to open/read/write files in Ocaml if these restrictions were not in place to know what things we need to replace.

let file = "flag.txt"
let () =
let ic = open_in file in
while true do
 let char = input_char ic in
 output_char stdout char;
 done

From this we know we at least need custom definitions for open_in, input_char, output_char, and stdout.

Making our custom functions

We can easily replace input_char and output_char with custom_input_char and custom_output_char respectively as a like-to-like replacement.
Looking at the source code open_in recursively keeps using other library functions which are also disabled, so we need to define all of them again. open_in uses open_in_gen which uses open_descriptor_in, open_desc and set_in_channel_name.
Finally those smelly nerds didn’t even leave stdout, so we need to re-define a custom_stdout which uses a custom_open_descriptor_out.

Final solution

let file = "flag.txt"

external custom_input_char : in_channel -> char = "caml_ml_input_char"
external custom_output_char : out_channel -> char -> unit = "caml_ml_output_char"

type open_flag =
 Open_rdonly | Open_wronly | Open_append
 | Open_creat | Open_trunc | Open_excl
 | Open_binary | Open_text | Open_nonblock

external custom_open_desc : string -> open_flag list -> int -> int = "caml_sys_open"
external custom_open_descriptor_in : int -> in_channel = "caml_ml_open_descriptor_in"
external custom_open_descriptor_out : int -> out_channel = "caml_ml_open_descriptor_out"
external custom_set_in_channel_name: in_channel -> string -> unit = "caml_ml_set_channel_name"

let custom_open_in_gen mode perm name =
 let c = custom_open_descriptor_in(custom_open_desc name mode perm) in
 custom_set_in_channel_name c name;
 c

let custom_open_in name =
 custom_open_in_gen [Open_rdonly; Open_text] 0 name

let custom_stdout = custom_open_descriptor_out 1

let () =

  let ic = custom_open_in file in

  try
    while true do
      let char = custom_input_char ic in
      custom_output_char custom_stdout char;
    done
  with End_of_file -> ()

Thank you for reading it, if you made it this far and have a great day! 😅

References

Static Typing in Ocaml: https://www2.lib.uchicago.edu/keith/ocaml-class/static.html
Detailed info on GADT’s: https://dev.realworldocaml.org/gadts.html
Some discussion on Ocaml pattern matching: https://discuss.ocaml.org/t/in-pattern-matching/2676
Ocaml stdlib source code: https://github.com/ocaml/ocaml/blob/trunk/stdlib/stdlib.ml
A bit about CTF Academy: https://ctf.asu.edu/education/ace-ctf-academy/

Stepping down into the Ocaml Mines - UIUCTF 2025 Writeup

Challenge #1: WeirdCaml

Category: revAuthor: n8

Brief info about the challenge and Ocaml

Taking a look at type puzzle

Solution

Making variables

Parsing conditions from constructors

Building constraints for Z3

Feeding constraints to Z3

Final solution:

Something to think about: Why does challenge say flag will be printed to stderr?

Challenge #2: Nocaml

Category: miscAuthor: n8

Solution

Making our custom functions

Final solution

References

Category: rev
Author: n8

Category: misc
Author: n8